
Production Possibility Frontiers
Production possibility frontiers
An opportunity cost will usually arise whenever an economic agent chooses between alternative ways of allocating scarce resources. The opportunity cost of such a decision is the value of the next best alternative use of scarce resources. Opportunity cost can be illustrated by using production possibility frontiers (PPFs) which provide a simple, yet powerful tool to illustrate the effects of making an economic choice.
A PPF shows all the possible combinations of two goods, or two options available at one point in time.
Production possibilities
Mythica, which is a hypothetical economy, produces only two goods – textbooks and computers. When it uses all of its resources, it can produce five million computers and fifty five million textbooks. In fact, it can produce all the following combinations of computers and books.
| COMPUTERS (m) | TEXTBOOKS (m) |
| 0 | 70 |
| 1 | 69 |
| 2 | 68 |
| 3 | 65 |
| 4 | 60 |
| 5 | 55 |
| 6 | 48 |
| 7 | 39 |
| 8 | 24 |
| 9 | 0 |
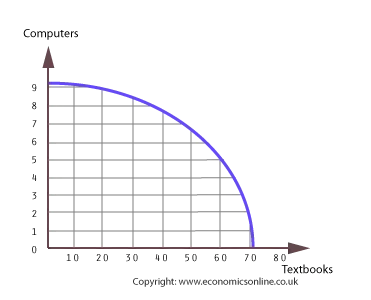
These combinations can also be shown graphically, the result being a production possibility frontier. The production possibility frontier (PPF) for computers and textbooks is shown here.
Interpreting PPFs
Firstly, we can describe the opportunity cost to Mythica of producing a given output of computers or textbooks. For example, If Mythica produces 3m computers; the opportunity cost is 5m textbooks. This is the difference between the maximum output of textbooks that can be produced if no computers are produced (which is 70m) and the number of textbooks that can be produced if 3m computers are produced (which is 65m). Similarly, the opportunity cost of producing 7m computers is 31m textbooks – which is 70 – 39.
PPFs can also illustrate the opportunity cost of a change in the quantity produced of one good. For example, suppose Mythica currently produces 3 million computers and 65m textbooks. We can calculate the opportunity cost to Mythica if it decides to increase production from 3 million computers to 7 million, shown on the PPF as a movement from point A to point B. and textbooks is shown here.

The result is a loss of output of 26 million textbooks (from 65 to 39m). Hence, the opportunity cost to Mythica of this decision can be expressed as 26m textbooks. In fact, this is the same as comparing the static opportunity cost of producing 3m computers (5m textbooks) and 7m computers (31m textbooks).
Pareto efficiency
Any point on a PPF, such as points ‘A’ and ‘B’, is said to be efficient and indicates that an economy’s scarce resources are being fully employed. This is also called Pareto efficiency, after Italian economist Vilfredo Pareto. Any point inside the PPF, such as point ‘X’ is said to be inefficient because output could be greater from the economy’s existing resources.
Any point outside the PPF, such as point ‘Z’, is impossible with the economy’s current scarce resources, but it may be an objective for the future. Pareto efficiency can be looked at in another way – when the only way to make someone better off is to make someone else worse off. In other words, Pareto efficiency means an economy is operating at its full potential, and no more output can be produced from its existing resources.

Pareto efficiency is unlikely to be achieved in the real world because of various rigidities and imperfections. For example, it is unlikely that all resources can be fully employed at any given point in time because some workers may be in the process of training, or in the process of searching for a new job. While searching for work, or being trained, they are unproductive. Similarly, an entrepreneur may have wound-up one business venture, and be in the process of setting-up a new one, but during this period, they are unproductive. Despite this, Pareto efficiency is still an extremely useful concept.
It is a useful concept for two reasons:
- It can be an objective for an economy because it can set a direction towards which an economy can move.
- It can help highlight the imperfections and rigidities that exist in an economy and prevent Pareto efficiency being achieved.
Productive and allocative efficiency
A point on a PPF is, by definition, productively efficient in that all of the economies resources are being fully employed, and their is no waste or unemployment. However, from the consumer’s (or society’s) point of view a particular combination of goods may not be allocatively efficient. For it to be allocatively efficient it must satisfy consumer demand and consumer preferences. As will be seen later, allocative efficiency is more formally expressed as a level of output where the marginal benefit to the consumer or the last unit consumed equals the marginal cost of supply of that unit. Clearly, not all combinations will satisfy this condition.
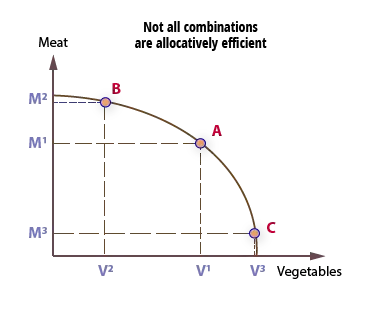
In the example shown, a society may produce only meat or vegetables, but its population prefers a varied diet. Hence, point A is likely to be much more allocatively efficient than point B and C, because these do not meet society’s preferences.
Increasing opportunity cost
Opportunity cost can be thought of in terms of how decisions to increase the production of an extra, marginal, unit of one good leads to a decrease in the production of another good.
According to economic theory, successive increases in the production of one good will lead to an increasing sacrifice in terms of a reduction in the other good. For example, as an economy tries to increase the production of good X , such as cameras, it must sacrifice more of the other good, Y, such as mobile phones.
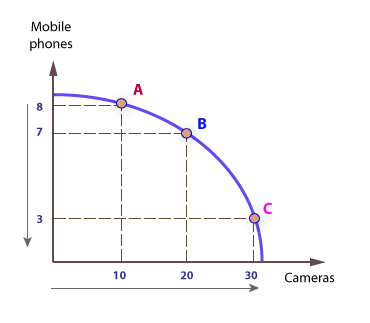
This explains why the PPF is concave to the origin, meaning its is bowed outwards. For example, if an economy initially produces at A, with 8m phones and 10m cameras (to 20m), and then increases output of cameras by 10m, it must sacrifice 1m phones, and it moves to point B.
If it now wishes to increase output of cameras by a further 10m (to 30m) it must sacrifice 2m phones, rather than 1m, and it moves to point C; hence, opportunity cost increases the more a good is produced.
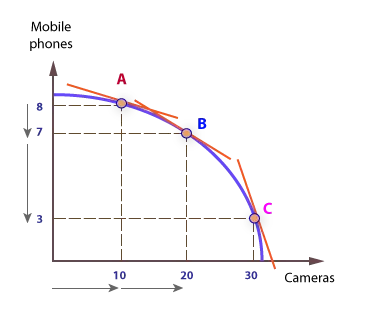
The gradient of the PPF gets steeper as more cameras are produced, indicating a greater sacrifice in terms of mobile phones foregone.
Marginal analysis
Economic decisions are taken in a marginal way, which means that decisions to produce, or consume, are made one at a time.
For example, a typical consumer does not decide to drink four cans of cola at the beginning of each day, rather they make four individual decisions, one at a time. Similarly, a baker does not decide to produce 5,000 loaves of bread in a year, but decides each day or week what to produce. Economic decisions are marginal because conditions are constantly changing, and consumers and producers would be highly irrational if they did not consider this. Hence, each production or consumption decision is assumed to be made one at a time so that changing conditions can be assessed.
Test your knowledge with a quiz
Press Next to launch the quiz
You are allowed two attempts – feedback is provided after
each question is attempted.
Go to: Economic growth


