
Game Theory
Game Theory
Game theory is widely regarded as having its origins in the mid-nineteenth century with the publication in 1838 of Augustin Cournot’s Researches into the Mathematical Principles of the Theory of Wealth, in which he attempted to explain the underlying rules governing the behaviour of duopolists. However, it was with the publication in 1944 of John von Neumann and Oskar Morgenstern’s The Theory of Games and Economic Behaviour that the modern principles of game theory were formulated. Game theory has been widely applied to the behaviour of producers with a few or only one competitor.
What is a game?
All games have the following:
- Rules, which govern conduct of the players
- Pay-offs, such as win, lose or draw
- Strategies, which influence the decision making process.
In applying game theory to the behaviour of firms we can suggest that firms face a number of strategic choices which govern their ability to achieve a desired pay-off, including:
Decisions on price and output, such as whether to:
- Raise
- Lower
- Hold
Decisions on products, such as whether to:
- Keep existing products
- Develop new ones
Decisions on promoting products, such as whether to:
- Spend more on advertising
- Spend less
- Keep spending constant
Firms could derive a range of possible pay-offs from their strategy choices, including:
- More profits for shareholders
- Greater market share
- Improved chances of survival
- Getting rid of a rival
The Prisoner’s Dilemma
The Prisoner’s Dilemma is a simple game which illustrates the choices facing oligopolies. The name ‘Prisoner’s Dilemma’ was first used in 1950 by Canadian mathematician, Albert W. Tucker when providing a simple example of game theory.
As you read the scenarios, you can play the part of one of the prisoners.
The scenario
Robin and Tom are prisoners:
They have been arrested for a petty crime, of which there is good evidence of their guilt – if found guilty they will receive a 2 year sentence.
During the interview the police officer becomes suspicious that the two prisoners are also guilty of a serious crime, but is not sure he has any evidence.
Robin and Tom are placed in separate rooms and cannot communicate with each other. The police officer tries to get them to confess to the serious crime by offering them some options, with possible pay-offs.
The options
Each is told that if they both confess to the serious crime they will receive a sentence of 3 years. However, each is also told that if he confesses and his partner does not, then he will get a light sentence of 1 year, and his partner will get 10 years. They know that if they both deny the serious offence they are certain to be found guilty of the lesser offence, and will get a 2 year sentence.
The pay-off matrix

What would you do if you were one of them? Give an answer before you read on.
The dilemma is that their own ‘pay-off’ is wholly dependent on the behaviour of the other prisoner. To avoid the worse-case scenario (10 years), the safest option is to confess and get 3 years. If collusion is possible they can both agree to deny (and get 2 years), but there is a very strong incentive to cheat because, if one denies and the other confesses, the best outcome of all is possible – that is 1 year. Fearing that the other may cheat, the safest option is to confess.
Types of strategy
Maximax
A maximax strategy is one where the player attempts to earn the maximum possible benefit available. This means they will prefer the alternative which includes the chance of achieving the best possible outcome – even if a highly unfavourable outcome is possible.
This strategy, often referred to as the best of the best is often seen as ‘naive’ and overly optimistic strategy, in that it assumes a highly favourable environment for decision making.
The best pay-off for Robin from confessing is 1 year (with Tom denying), and the best pay-off from denying is 2 years (with Tom denying) – so the best of the best is to confess (I year).
Maximin
A maximin strategy is where a player chooses the best of the worst pay-off. This is commonly chosen when a player cannot rely on the other party to keep any agreement that has been made – for example, to deny. In the Prisoner’s Dilemma, the worst pay-off to Robin from confessing is to get 3 years (with Tom confessing), and the worst pay-off from denying is 10 years (with Tom confessing) – therefore the best of the worst is to confess.
In this case, both the maximin and maximax strategies would be to confess. When this occurs, it is said to be the dominant strategy.
Dominant strategy
A dominant strategy is the best outcome irrespective of what the other player chooses, in this case it is for each player to confess – both the optimistic maximax and pessimistic maximin lead to the same decision being taken.
How does this relate to a firm’s behaviour?
In general, game theory suggests that firms are unlikely to trust each other, even if they collude and come to an agreement such as raising price together.
Consider the hypothetical example of two Airlines and return ticket prices to New York.
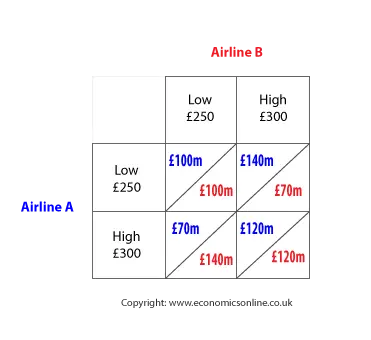
In this case, for both Airlines, the aggressive maximax strategy is £140m from a low price and £120m from a high price, so a low price gives the maximax pay-off.
In terms of the pessimistic maximin strategy, the worst outcome from a low price is £100m, and from a high price is £70m – hence a low price provides the best of the worst outcomes.
Again, lowering price is the dominant strategy, and the only way to increase the pay-off would be to collude and increase price together. Of course, this requires an agreement, and collusion, and this creates two further risks – one of the airlines reneges on the agreement and ‘rats’, and the competition authorities investigate the airlines, and impose a penalty.
Nash equilibrium
Nash equilibrium, named after Nobel winning economist, John Nash, is a solution to a game involving two or more players who want the best outcome for themselves and must take the actions of others into account. When Nash equilibrium is reached, players cannot improve their payoff by independently changing their strategy. This means that it is the best strategy assuming the other has chosen a strategy and will not change it. For example, in the Prisoner’s Dilemma game, confessing is a Nash equilibrium because it is the best outcome, taking into account the likely actions of others.
Implications
Game Theory provides many insights into the behaviour of oligopolists. For example, it indicates that generating rules for behaviour may take some of the risks out of competition, such as:
- Employing a simple cost-plus pricing method which is shared by all participants. This would work well in situations where oligopolists share similar or identical costs, such as with petrol retailing.
- Implicitly agreeing a ‘price leader’ with other firms as followers. In the Airline example, firm A may lead and raise price, with B passively following suit. In this case, both would generate revenues of £120.
- Supermarkets implicitly agreeing some lines where price cutting will take place, such as bread or baked beans, but keeping price constant for most lines.
- Generally keeping prices stable (sticky) to avoid price retaliation.
See: Oligopoly


