Oligopoly

Updated September 14th, 2022

Defining and measuring oligopoly

An oligopoly is a market structure in which a few firms dominate. When a market is shared between a few firms, it is said to be highly concentrated. Although only a few firms dominate, it is possible that many small firms may also operate in the market. Some examples of oligopolies include the car industry, petrol retail, pharmaceutical industry, coffee shop retail, and airlines. In each of these industries, a few large companies dominate. Considering the market for air travel,  major airlines like British Airways(BA) and Air France often operate their routes with only a few close competitors, but there are also many small airlines catering for the holidaymaker or offering specialist services. Similarly, while the 'Big Six' energy suppliers dominate the UK market, with a combined market share of 78% for electricity supply (according to the energy regulator, Ofcom, there are currently 54 active suppliers. (2017 data).

Concentration ratios

Oligopolies may be identified using concentration ratios, which measure the proportion of total market share controlled by a given number of firms. When there is a high concentration ratio in an industry, economists tend to identify the industry as an oligopoly.

Example of a hypothetical concentration ratio

The following are the annual sales, in £m, of the six firms in a hypothetical market:

A = 56
B = 43
C = 22
D = 12
E = 3
F = 1

In this hypothetical case, the 3-firm concentration ratio is 88.3%, that is 121/137 x 100.

Examples

Fixed Broadband services

Fixed broadband supply in the UK is dominated by four main suppliers - BT (with a market share of 32%), Virgin Media (at 20%), Sky (at 22%) and TalkTalk (at 14%), making a four-firm concentration ratio of 86% (2015). Source: OFCOM.

Fuel retailing

Fuel retailing in the UK is dominated by six major suppliers, including Tesco, BP, Shell, Esso, Morrisons and Sainsbury.

Further examples

Cinema attendances Banking

The Herfindahl – Hirschman Index (H-H Index)

This is an alternative method of measuring concentration and for tracking changes in the level of concentration following mergers. The H-H index is found by adding together the squared values of the % market shares of all the firms in the market. For example, if three firms exist in the market the formula is X² + Y² + Z²; where X, Y and Z are the percentages of the three firm’s market shares. If the index is below 1000, the market is not considered concentrated, while an index above 2000 indicates a highly concentrated market or industry – the higher the figure the greater the concentration. Mergers between oligopolists increase concentration and ‘monopoly power’ and are likely to be the subject of regulation.

Key characteristics

The main characteristics of firms operating in a market with few close rivals include:

Interdependence

Firms operating under conditions of oligopoly are said to be interdependent , which means they cannot act independently of each other. A firm operating in a market with just a few competitors must take the potential reaction of its closest rivals into account when making its own decisions. In the case of petrol retailing, a seller like Texaco may wish increase its market share by reducing price, but it must take into account the possibility that close rivals, such as Shell and BP, who may also reduce their price in retaliation. An understanding of game theory and the Prisoner’s Dilemma helps appreciate the concept of interdependence.

Strategy

Strategy is extremely important to firms that are interdependent. Because firms cannot act independently, they must anticipate the likely response of a rival to any given change in their price, or their non-price activity. In other words, they need to plan, and work out a range of possible options based on how they think rivals might react. Oligopolists have to make critical strategic decisions, such as:

• Whether to compete with rivals, or collude with them.
• Whether to raise or lower price, or keep price constant.
• Whether to be the first firm to implement a new strategy, or whether to wait and see what rivals do. The advantages of ‘going first’ or ‘going second’ are respectively called 1st and 2nd-mover advantage. Sometimes it pays to go first because a firm can generate head-start profits. 2nd mover advantage occurs when it pays to wait and see what new strategies are launched by rivals, and then try to improve on them or find ways to undermine them.

Barriers to entry

Oligopolies and monopolies frequently maintain their position of dominance in a market might because it is too costly or difficult for potential rivals to enter the market. These hurdles are called barriers to entry and the incumbent can erect them deliberately, or they can exploit natural barriers that exist.

Natural entry barriers include:

Economies of large scale production.

If a market has significant economies of scale that have already been exploited by the incumbents, new entrants are deterred.

Ownership or control of a key scarce resource

Owning scarce resources that other firms would like to use creates a considerable barrier to entry, such as an airline controlling access to an airport.

High set-up costs

High set-up costs deter initial market entry, because they increase break-even output, and delay the possibility of making profits.  Many of these costs are sunk costs, which are costs that cannot be recovered when a firm leaves a market, and include marketing and advertising costs and other fixed costs.

High R&D costs

Spending money on Research and Development (R & D) is often a signal to potential entrants that the firm has large financial reserves. In order to compete, new entrants will have to match, or exceed, this level of spending in order to compete in the future. This deters entry, and is widely found in oligopolistic markets such as pharmaceuticals and the chemical industry.

Artificial barriers include:

Predatory pricing

Predatory pricing occurs when a firm deliberately tries to push prices low enough to force rivals out of the market.

Limit pricing

Limit pricing means the incumbent firm sets a low price, and a high output, so that entrants cannot make a profit at that price.  This is best achieved by selling at a price just below the average total costs (ATC) of potential entrants. This signals to potential entrants that profits are impossible to make.

Superior knowledge

An incumbent may, over time, have built up a superior level of knowledge of the market, its customers, and its production costs. The superior knowledge of an incumbent can give it considerable competitive advantage over a potential entrant.

Predatory acquisition

Predatory acquisition involves taking-over a potential rival by purchasing sufficient shares to gain a controlling interest, or by a complete buy-out. As with other deliberate barriers, regulators, like the Competition and Markets Authority (CMA), may prevent this because it is likely to reduce competition.

Advertising

Advertising is another sunk cost - the more that is spent by incumbent firms the greater the deterrent to new entrants.

A strong brand

A strong brand creates loyalty, ‘locks in’ existing customers, and deters entry.

Loyalty schemes

Schemes such as Tesco’s Club Card, help oligopolists retain customer loyalty and deter entrants who need to gain market share.

Exclusive contracts, patents and licences

These make entry difficult as they favour existing firms who have won the contracts or own the licenses. For example, contracts between suppliers and retailers can exclude other retailers from entering the market.

Vertical integration

Vertical integration can ‘tie up’ the supply chain and make life tough for potential entrants, such as an electronics manufacturer like Sony having its own retail outlets (Sony Centres). Vertical integration in the media industry is widspread, with Netflix having purchsed the US based ABQ studios in 2018, and completing an agreement in 2019 with the UK's Pinewood studio group giving it access to 14 sound stages, workshops, and office space.

Collusive oligopolies

Another key feature of oligopolistic markets is that firms may attempt to collude, rather than compete. If colluding, participants act like a monopoly and can enjoy the benefits of higher profits over the long term.

Types of collusion

Overt

Overt collusion occurs when there is no attempt to hide agreements, such as the when firms form trade associations like the Association of Petrol Retailers.

Covert

Covert collusion occurs when firms try to hide the results of their collusion, usually to avoid detection by regulators, such as when fixing prices.

Tacit

Tacit collusion (also called 'rule-based' collusion) arises when firms act together, called 'acting in concert'  but where there is no formal or even informal agreement. For example, it may be accepted that a particular firm is the price leader in an industry, and other firms simply follow the lead of this firm. All firms may ‘understand’ this, but no agreement or record exists to prove it. If firms do collude, and their behaviour can be proven to result in reduced competition, they are likely to be subject to regulation. In many cases, tacit collusion is difficult or impossible to prove, though regulators are becoming increasingly sophisticated in developing new methods of detection.

Competitive oligopolies

When competing, oligopolists prefer non-price competition in order to avoid price wars. A price reduction may achieve strategic benefits, such as gaining market share, or deterring entry, but the danger is that rivals will simply reduce their prices in response. This leads to little or no gain, but can lead to falling revenues and profits. Hence, a far more beneficial strategy may be to undertake non-price competition.

Pricing strategies of oligopolies

Oligopolies may pursue the following pricing strategies:

1. Oligopolists may use predatory pricing to force rivals out of the market. This means keeping price artificially low, and often below the full cost of production.
2. They may also operate a limit-pricing strategy to deter entrants, which is also called entry forestalling price.
3. Oligopolists may collude with rivals and raise price together, but this may attract new entrants.
4. Cost-plus pricing is a straightforward pricing method, where a firm sets a price by calculating average production costs and then adding a fixed mark-up to achieve a desired profit level. Cost-plus pricing is also called rule of thumb pricing.There are different versions of cost-pus pricing, including full cost pricing, where all costs - that is, fixed and variable costs - are calculated, plus a mark up for profits, and contribution pricing, where only variable costs are calculated with precision and the mark-up is a contribution to both fixed costs and profits.

Cost-plus pricing is very useful for firms that produce a number of different products, or where uncertainty exists. It has been suggested that cost-plus pricing is common because a precise calculation of marginal cost and marginal revenue is difficult for many oligopolists. Hence, it can be regarded as a response to information failure. Cost-plus pricing is also common in oligopoly markets because it is likely that the few firms that dominate may often share similar costs, as in the case of petrol retailers. However, there is a risk with such a rigid pricing strategy as rivals could adopt a more flexible discounting strategy to gain market share. Cost-plus pricing can also be explained through the application of game theory. If one firm uses cost-plus pricing - perhaps the dominant firm with the greatest market share - others may follow-suit so that the strategy becomes a shared one, which acts as a pricing rule. This takes some of the risk out of pricing decisions, given that all firms will abide by the rule. This could be considered a form of tacit collusion.

Non-price strategies

Non-price competition is the favoured strategy for oligopolists because price competition can lead to destructive price wars – examples include:

1. Trying to improve quality and after sales servicing, such as offering extended guarantees.
2. Spending on advertising, sponsorship and product placement - also called hidden advertising – is very significant to many oligopolists. The UK's football Premiership has long been sponsored by firms in oligopolies, including Barclays Bank and Carling.
3. Sales promotion, such as buy-one-get-one-free (BOGOF), is associated with the large supermarkets, which is a highly oligopolistic market, dominated by three or four large chains.
4. Loyalty schemes, which are common in the supermarket sector, such as Sainsbury’s Nectar Card and Tesco’s Club Card.

Each strategy can be evaluated in terms of:

1. How successful is it likely to be?
2. Will rivals be able to copy the strategy?
3. Will the firms get a 1st - mover advantage?
4. How expensive is it to introduce the strategy? If the cost of implementation is greater than the pay-off, clearly it will be rejected.
5. How long will it take to work? A strategy that takes five years to generate a pay-off may be rejected in favour of a strategy with a quicker pay-off.

Price stickiness

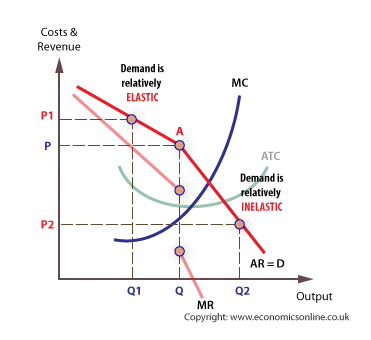
The theory of oligopoly suggests that, once a price has been determined, will stick it at this price. This is largely because firms cannot pursue independent strategies. For example, if an airline raises the price of its tickets from London to New York, rivals will not follow suit and the airline will lose revenue - the demand curve for the price increase is relatively elastic. Rivals have no need to follow suit because it is to their competitive advantage to keep their prices as they are. However, if the airline lowers its price, rivals would be forced to follow suit and drop their prices in response. Again, the airline will lose sales revenue and market share. The demand curve is relatively inelastic in this context.

Kinked demand curve

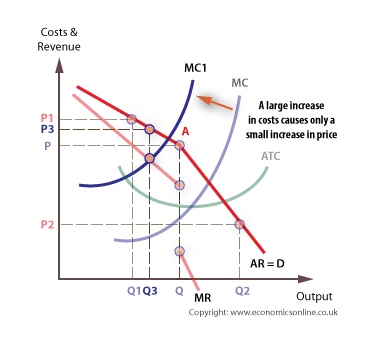
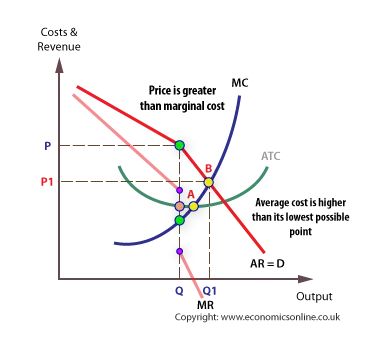
The reaction of rivals to a price change depends on whether price is raised or lowered. The elasticity of demand, and hence the gradient of the demand curve, will be also be different. The demand curve will be kinked, at the current price. Even when there is a large rise in marginal cost, price tends to stick close to its original, given the high price elasticity of demand for any price rise. At price P, and output Q, revenue will be maximised.

Maximising profits

If marginal revenue and marginal costs are added it is possible to show that profits will also be maximised at price P. Profits will always be maximised when MC = MR, and so long as MC cuts MR in its vertical portion, then profit maximisation is still at P. Furthermore, if MC changes in the vertical portion of the MR curve, price still sticks at P. Even when MC moves out of the vertical portion, the effect on price is minimal, and consumers will not gain the benefit of any cost reduction.

A game theory approach to price stickiness

Pricing strategies can also be looked at in terms of game theory; that is in terms of strategies and payoffs. There are three possible price strategies, with different pay-offs and risks:

• Raise price
• Lower price
• Keep price constant

The choice of strategy will depend upon the pay-offs, which depends upon the actions of competitors. Raising price or lowering price could lead to a beneficial pay-off, but both strategies can lead to losses, which could be potentially disastrous. In short, changing price is too risky to undertake. Therefore, although keeping price constant will not lead to the single best outcome, it may be the least risky strategy for an oligopolist.

The Prisoner’s Dilemma

Game theory also predicts that: There is a tendency for cartels to form because co-operation is likely to be highly rewarding. Co-operation reduces the uncertainty associated with the mutual interdependence of rivals in an oligopolistic market. While cartels are ‘unlawful’ in most countries, they may still operate, with members concealing their unlawful behaviour. Cartels are designed to protect the interests of members, and the interests of consumers may suffer because of:

1. Higher prices or hidden prices, such as the hidden charges in credit card transactions
2. Lower output
3. Restricted choice or other limiting conditions associated with the transaction

A classic game called the Prisoner's Dilemma is often used to demonstrate the interdependence of oligopolists.

Examples of Oligopoly

Oligopolies are common in the airline industry, banking, brewing, soft-drinks, supermarkets and music.  For example, the manufacture, distribution and publication of music products in the UK, as in the EU and USA, is highly concentrated, with a 3-firm concentration ratio of around 70%, and is usually identified as an oligopoly.

Evaluation of oligopolies

Oligopolies are significant because they generate a considerable share of the UK’s national income, and they dominate many sectors of the UK economy.

The disadvantages of oligopolies

Oligopolies can be criticised on a number of obvious grounds, including:

1. High concentration reduces consumer choice.
2. Cartel-like behaviour reduces competition and can lead to higher prices and reduced output.
3. Given the lack of competition, oligopolists may be free to engage in the manipulation of consumer decision making. By making decisions more complex - such as financial decisions about mortgages - individual consumers fall back on heuristics and rule of thumb processes, which can lead to decision making bias and irrational behaviour, including making purchases which add no utility or even harm the individual consumer.
4. Firms can be prevented from entering a market because of deliberate barriers to entry.
5. There is a potential loss of economic welfare.
6. Oligopolists may be allocatively and productively inefficient.

Oligopolies tend to be both allocatively and productively inefficient. At profit maximising equilibrium, P, prce is above MC, and output, Q, is less than the productively efficient output, Q1, at point A.

The advantages of oligopolies

However, oligopolies may provide the following benefits:

1. Oligopolies may adopt a highly competitive strategy, in which case they can generate similar benefits to more competitive market structures, such as lower prices. Even though there are a few firms, making the market uncompetitive, their behaviour may be highly competitive.
2. Oligopolists may be dynamically efficient in terms of innovation and new product and process development. The super-normal profits they generate may be used to innovate, in which case the consumer may gain.
3. Price stability may bring advantages to consumers and the macro-economy because it helps consumers plan ahead and stabilises their expenditure, which may help stabilise the trade cycle.

Test your knowledge with a quiz

---

Press Next to launch the quiz

You are allowed two attempts - feedback is provided after each question is attempted.

---

Press Next to launch the quiz

You are allowed two attempts - feedback is provided after each question is attempted.

See Transfer pricing See Browser market shares