
An image of a girl eating food.
Equimarginal Principle
Statement
The equimarginal principle states that by keeping other things constant, if a consumer spends his income on different commodities, he or she will get maximum satisfaction when marginal utility per unit of money is the same for each commodity.
This principle is also known as the law of substitution or the law of maximum satisfaction.
This principle is used to find consumer equilibrium when a consumer consumes multiple commodities.
Origin
The equimarginal principle is explained by many economists and given due importance. This concept was first introduced by H. H. Gossen, a Prussian Civil Servant (1810–1858), and was further popularised by British economist Alferd Marshall. This principle is basically an extension of the law of diminishing marginal utility in managerial economics.
Equation
Assuming that a consumer is consuming two goods, A and B, the equation or formula for consumer equilibrium is as follows:

The consumer will be in equilibrium, and his or her total utility will be maximised, when the above equation is satisfied. MU/price is called the marginal utility of expenditure on each unit of good.
Assumptions
The equimarginal principle has the following assumptions:
Multiple Commodities
The consumer is consuming two goods, A and B.
Cardinality
Utility can be measured numerically.
Rationality
The consumer is a rational decision maker.
Prices
The prices of goods A and B are constant.
Income
The money income of the consumer is constant.
Marginal Utility of Money
The marginal utility of money is constant.
Taste and Fashion
Taste and fashion remain constant during the period of consumption.
Size of Commodity
The units of goods A and B are of reasonable size.
Objective
The objective of the consumer is to maximise total utility.
Basic Terms
Utility
The power of a commodity to satisfy a human want is called utility.
Marginal Utility (MU)
The extra satisfaction gained by a consumer from the consumption of an extra unit of a commodity is called its marginal utility.
Total Utility (TU)
Total satisfaction gained by a consumer from the consumption of a given quantity of a commodity is called total utility.
Cardinal Utility
The utility that can be measured numerically is called cardinal utility. Its unit of measurement is called `Util’.
Consumer Equilibrium
A consumer is said to be in equilibrium when he/she allocates income in such a way that total satisfaction is maximised and there is no tendency to change that state.
Understanding the Equimarginal Principle with a Data Example
Suppose that the consumer has a constant money income of $5 and the price of each of goods A and P is $1. The following data is also assumed:
|
Quantity of A |
MU of A |
Quantity of B |
MU of B |
|
0 |
--- |
0 |
--- |
|
1 |
12 |
1 |
14 |
|
2 |
10 |
2 |
12 |
|
3 |
8 |
3 |
10 |
|
4 |
6 |
4 |
8 |
|
5 |
4 |
5 |
6 |
Now let’s calculate the marginal utility per unit of money for each commodity.
|
Quantity of A |
MU of A/Price of A |
Quantity of B |
MU of B/Price of B |
|
0 |
--- |
0 |
--- |
|
1 |
12 |
1 |
14 |
|
2 |
10 |
2 |
12 |
|
3 |
8 |
3 |
10 |
|
4 |
6 |
4 |
8 |
|
5 |
4 |
5 |
6 |
The equation of the marginal utility principle is satisfied for 2 units of good A and 3 units of good B. Also, all of the consumer income ($5) is spent on this combination. Hence, the consumer should consume 2 units of A and 3 units of B to maximise total utility (TU).
Application of the Marginal Utility Principle
Case 1: When MU of A/Price of A > MU of B/Price of B
In this situation, the consumer is not in equilibrium. The consumer is getting a higher MU from the last $ spent on good A than from good B. So, the consumer will reallocate his spending by increasing the quantity of good A and decreasing the quantity of good B. In this way, consumer equilibrium will be achieved.
Case 2: When MU of A/Price of A = MU of B/Price of B
In this situation, the consumer is in equilibrium, and there is no tendency to change that state. The consumer is getting the same MU from the last $ spent on good A and on good B. So, the consumer is getting the maximum TU.
Case 3: When MU of A/Price of A < MU of B/Price of B
In this situation, the consumer is not in equilibrium. The consumer is getting a higher MU from the last $ spent on good B than from good A. So, the consumer will reallocate his spending by increasing the quantity of good B and decreasing the quantity of good A. In this way, consumer equilibrium will be achieved.
Derivation of Demand Curve
The consumer equilibrium, according to the law of equimarginal utility, is where
MU of A/Price of A = MU of B/Price of B.
If the price of good A is decreased, then MU of A/Price of A will be greater than MU of B/Price of B.
In this situation, the consumer is getting a higher MU from the last $ spent on good A than from good B. So, the consumer will reallocate his spending by increasing the quantity of good A and decreasing the quantity of good B.
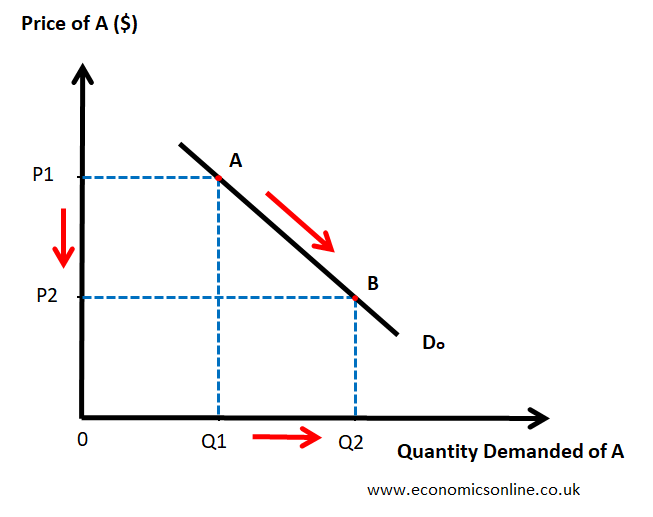
Hence, the quantity of good A will increase as a result of a decrease in its price. This explains the inverse relationship between the price of good A and its quantity demanded, which can also be represented by the following downward-sloping demand curve. The quantity demanded of good A is taken on the horizontal axis (X-axis), and the price of good A is taken on the vertical axis (Y-axis).
Limitations of Equimarginal Principle
Despite its merits, the equimarginal principle has a few limitations:
Cardinality
The equimarginal principle assumes that the utility is cardinal and it can be numerically. In reality, this is not true. There is no device invented so far which can measure utility.
Rationality
The equimarginal principle assumes that the consumer is a rational decision maker with perfect information, which may not always be the case in the real world. The consumer may consume goods out of a habit or may purchase them under the influence of adverting or impulse.
Prices
The prices of goods A and P may not be constant.
Size of the Commodity
The equimarginal principle assumes that the units of goods A and B are of reasonable size. Yet, in real life, goods may be of a larger size, for example, a car.
Conclusion
The equimarginal principle is a key concept in economics, and it serves as a powerful tool for optimising resource allocation. By equalising the marginal utility across different products, consumers can make rational decisions to maximise their total satisfaction. While the principle has its limitations, its application can lead to better allocation of resources and improved decision-making.


