
An image of a person throwing a dart pin.
Midpoint Method in Economics
Introduction
The midpoint method in economics is used to calculate the price elasticity of demand by taking the average values of price and quantity demanded. The midpoint elasticity is also called the arc elasticity. To accurately understand the concept of the midpoint method, let us first understand some basic terms:
Basic Terms
Elasticity
The responsiveness of one variable to the change in another variable is called elasticity in economics. Two main types of elasticity are the elasticity of demand and the elasticity of supply.
Elasticity of Demand
The responsiveness of the quantity demanded of a good to the change in any variable affecting demand is called price elasticity of demand. Some types of elasticity of demand are price elasticity of demand (PED), income elasticity of demand (YED), cross elasticity of demand (XED), and advertising elasticity of demand (AED). In this article, we will focus on using the midpoint formula for calculating the price elasticity of demand.
Price Elasticity of Demand (PED)
The responsiveness of the quantity demanded of a good concerning the change in its price is called price elasticity of demand. The following formula is used to calculate PED.

This formula calculates PED by using the ratio between the percent change in quantity demanded and the percent price change. This is the basic formula to calculate PED.
Price elasticity tells us about the price sensitivity of consumers. When the quantity demanded for products or services significantly changes as the price changes, this means that the demand is elastic, but when the quantity demanded changes a bit, then the demand is called inelastic.
Price Elastic Demand
In economics, the word “elastic” means something receptive or responsive to change in some factors. When a small percentage change in the price of a product leads to a large percentage change in its quantity demanded, the demand is said to be price elastic. For elastic demand, the magnitude (value after ignoring the negative sign) of PED is greater than 1. Price elastic demand means that consumers have high responsiveness to price change.
Price Inelastic Demand
In economics, the word “inelastic” means something that is not very receptive or responsive to change in some factors. When a large percentage change in the price of a product leads to a small change in its quantity demanded, the demand is said to be price inelastic. For inelastic demand, the elasticity measure or the magnitude (value after ignoring the negative sign) of PED is less than 1. Price inelastic demand means that consumers have low responsiveness to price changes.
Unitary Price Elasticity of Demand
In economics, the term “unitary” means the elasticity of something is exactly equal to 1. In a unitary situation, the percentage change in quantity demanded is equal to the percentage change in price. A unitary elasticity of demand explains that the change in quantity demanded of a good is in the same percentage as the change in its price. Price unit elastic demand means that consumers have proportional responsiveness to price changes.
Formula of the Midpoint Method
The formula for the midpoint method is:
Midpoint Method = (Change in Quantity/Average Quantity) / (Change in Price / Average Price)

Here,
P1 is the initial price, or the first price point.
P2 is the final price, or the second price point.
Q1 is the initial quantity demanded, or the first quantity point.
Q2 is the final quantity demanded, or the second quantity point.
Now let’s relate this midpoint formula to the basic formula of PED.
PED = % Change in Quantity Demanded / % Change in Price
% Change in Quantity Demanded = (Change in Quantity Demanded / Average Quantity Demanded) x 100
% Change in Price = (Change in Price / Average Price) x 100
By putting these values in the basic formula of PED, we get the midpoint formula of PED.
Here, we have used the average values of the price and the quantity demanded to find the % changes which are actually the midpoint values. This gives us the logic behind the name of the midpoint formula.
Steps to Calculate the Midpoint Elasticity
The following steps are used to compute the midpoint elasticity, which are explained as follows:
Make the Demand Schedule or the Demand Curve
In order to calculate PED by using the midpoint method, we must have the demand schedule or the demand curve. Both of them will give us the initial and final values of the price and the quantity demanded using the midpoint formula.
Determine the Initial Quantity and Price
Now, we have to identify the initial point on the demand curve and write down the values of quantity and price.
Determine the Final Quantity and Price
Now, we have to identify the final point on the demand curve and write down the values of quantity and price.
Use the Midpoint Formula to Calculate PED
We put both the values of price and quantity demanded in the midpoint formula to calculate PED. The change in price or quantity demanded is calculated by subtracting the old value from the new value. Average values are used in the denominators. A calculator can be used to do the math.
Ignore the Negative Sign
Once the PED is calculated, we ignore the negative sign with elasticity value, in order to make it more useful. This will be the absolute value of the result of PED, the coefficient of PED or the magnitude of the elasticity.
Analyse the Result
After ignoring the negative sign, we use the following criteria to analyse the result.
If PED>1, demand is price elastic.
If PED<1, demand is price inelastic.
If PED=1, demand is unit elastic.
Remember that the elasticity answer is always interpreted in the percentage terms.
Example of the Midpoint Method
Suppose the price of a T-shirt is $14, and the quantity demanded of this T-shirt is 60 units. But after an increase in the price of the T-shirt from $14 to $16, the quantity demanded for this T-shirt decreased from 60 units to 40 units. In this example,
P1 = $14
P2 = $16
Q1 = 60 units
Q2 = 40 units
Now, let’s use the midpoint formula to calculate the price elasticity of demand for T-shirts.
Price Elasticity of Demand = (Change in Quantity/Average Quantity) / (Change in Price / Average Price)
Firstly, we need to calculate the values of average quantity and average price.
Average quantity demanded = (60+40/2) = 50 units.
Average price = (14+16/2) = $15.
Now, let’s put the values in the midpoint formula:
Price Elasticity of Demand = (40-60/50) / (16-14/15) = (-20/50) / (2/15) = -0.4 / 0.1333 = -3.0007
The negative sign shows that there is an inverse relationship between the price of T-shirt and its quantity demanded, according to the law of demand. The price and the quantity demanded move in opposite directions.
The magnitude of PED is 3.0007 which is greater than 1, indicating that the demand for T-shirts is elastic and consumers are responsive to the change in the price of T-shirts.
Understanding the Midpoint Method
Let’s understand the midpoint method by using the graph of the demand curve.
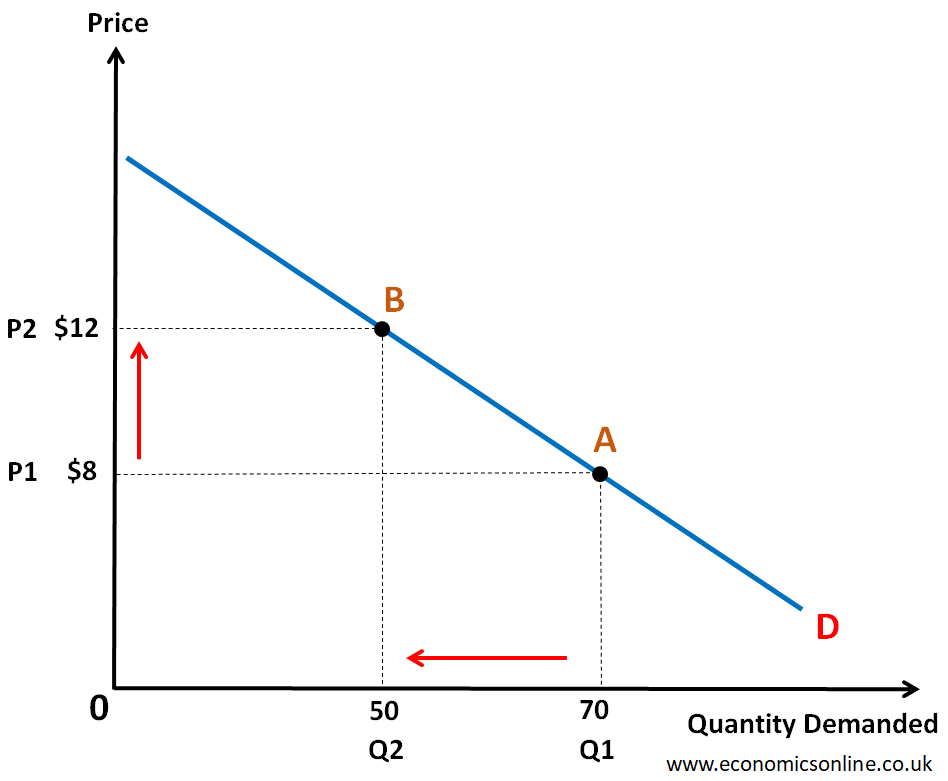
In the above graph, we have the quantity demanded on the horizontal axis (x-axis) and the price on the vertical axis (y-axis). At point A, when the price is $8, the quantity demanded is 70 units. At point B, when the price is $12, the quantity demanded is 50 units. This graph tells us that if we increase the price, the quantity demand decreases. So, here is the data.
P1 = $8
P2 = $12
Q1 = 70 units
Q2 = 50 units
Now, let’s use the midpoint formula to calculate the midpoint elasticity between two points A and B on the demand curve.
Firstly, we need to calculate the values of average quantity and average price.
Average quantity demanded = (70+50/2) = 60 units.
Average price = (8+12/2) = $10.
Now, let’s put the values in the midpoint formula:
Price Elasticity of Demand = (50-70/60) / (12-8/10) = (-20/60) / (4/10) = -0.33 / 0.4 = -0.83
The magnitude of PED is 0.83 over this interval, which is less than 1, indicating that the demand is inelastic.
Point Elasticity of Demand
A common formula to calculate price elasticity of demand between two points is the point elasticity formula, which is given below.

Now let’s relate this point elasticity formula to the basic formula of PED.
PED = % Change in Quantity Demanded / % Change in Price
% Change in Quantity Demanded = (Change in Quantity Demanded / Initial Quantity Demanded) x 100
% Change in Price = (Change in Price / Initial Price) x 100
By putting these values in the basic formula of PED, we get the point elasticity formula of PED.
Here, we have used the initial values of the price and the quantity demanded to find the % changes instead of using the average values (midpoint method).
The Problem with the Point Elasticity Formula
Let’s suppose that we are calculating PED between two points A and B on the demand curve. The problem with the point elasticity formula is that it gives different answers of PED when we calculate it from point A to B and from point B to A. This problem is solved by using the midpoint method.
Midpoint Elasticity vs. Point Elasticity
Let’s take an example, to compare the use of midpoint formula and point elasticity formula.
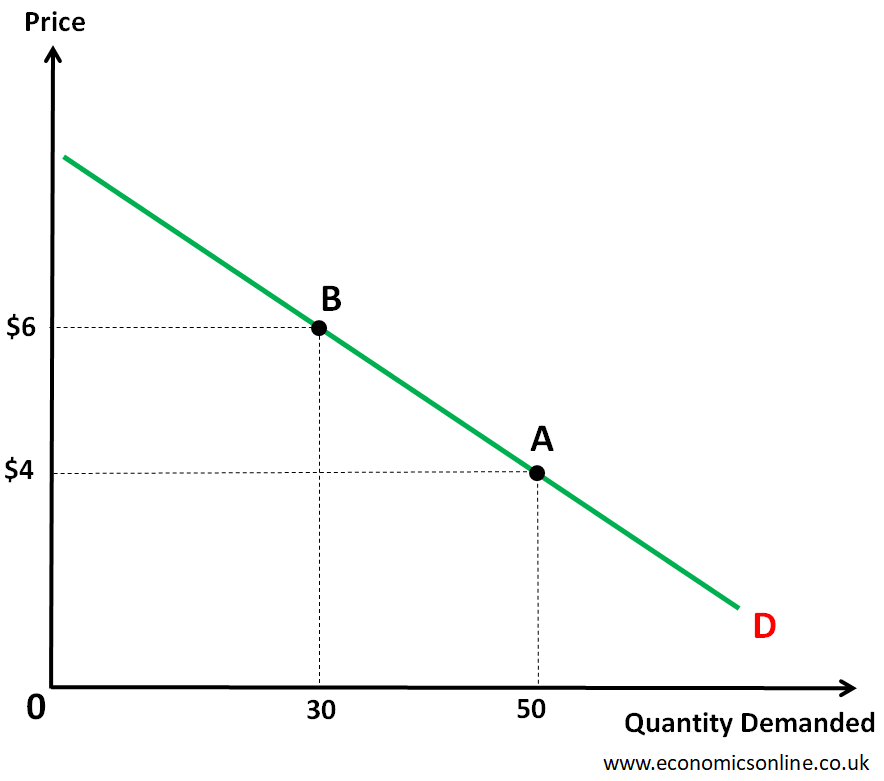
Point Elasticity: From Point A to B
If we take the initial point as A and the final point as B, then the data values are:
P1 = $4
P2 = $6
Q1 = 50 units
Q2 = 30 units
Now, let’s put the values in the point elasticity formula:
Point Elasticity = (30-50/50) / (6-4/4) = (-20/50) / (2/4) = -0.4 / 0.5 = -0.8
The magnitude of PED is 0.8 which is less than 1, indicating that the demand is price inelastic.
Point Elasticity: From Point B to A
If we take the initial point as B and the final point as A, then the data values are:
P1 = $6
P2 = $4
Q1 = 30 units
Q2 = 50 units
Now, let’s put the values in the point elasticity formula:
Point Elasticity = (50-30/30) / (4-6/6) = (20/30) / (-2/6) = 0.667 / -0.333 = -2
The magnitude of PED is 2 which is greater than 1, indicating that the demand is price elastic.
Point Elasticity: Result
In both of the above cases, the answer of PED is different because price elasticity of demand changes at different points with the change in the initial point. From point A to B, we have a small numerator and a large denominator, while from point B to A, we have a large numerator and a small denominator. This is the problem with point elasticity formula. This problem is solved by using midpoint method.
Midpoint Elasticity: From Point A to B
If we take the initial point as A and the final point as B, then the data values are:
P1 = $4
P2 = $6
Q1 = 50 units
Q2 = 30 units
Firstly, we need to calculate the values of average quantity and average price.
Average quantity demanded = (30+50/2) = 40 units.
Average price = (4+6/2) = $5.
Now, let’s put the values in the midpoint formula:
Midpoint Elasticity = (30-50/40) / (6-4/5) = (-20/40) / (2/5) = -0.5 / 0.4 = -1.25
The magnitude of PED is 1.25 which is greater than 1, indicating that the demand is price elastic.
Midpoint Elasticity: From Point B to A
If we take the initial point as B and the final point as A, then the data values are:
P1 = $6
P2 = $4
Q1 = 30 units
Q2 = 50 units
Firstly, we need to calculate the values of average quantity and average price.
Average quantity demanded = (30+50/2) = 40 units.
Average price = (4+6/2) = $5.
Now, let’s put the values in the midpoint formula:
Midpoint Elasticity = (50-30/40) / (4-6/5) = (20/40) / (-2/5) = 0.5 / -0.4 = -1.25
The magnitude of PED is 1.25 which is greater than 1, indicating that the demand is price elastic.
Midpoint Elasticity: Result
In both of the above cases, the answer of PED is the same, which is -1.25. This is the advantage of the midpoint method.
Purpose of the Midpoint Method
The purpose of the midpoint method is explained as follows:
Precise Elasticity Measurement
The midpoint method’s purpose is to provide precise and accurate measurement by estimating average values of quantity and price. The midpoint method is used to quantify the price elasticity of demand between two points irrespective of whether the price drops or rises.
Eliminates Bias
The midpoint method is used to eliminate the bias that happens when we use the traditional method or formula for calculating the corresponding percent change. This explains that elasticity does not depend on the initial or final points of a curve.
Consistent Comparison
The midpoint method is used for a consistent comparison of elasticity between different price ranges with the help of average values. Consistent comparison provides a systematized approach to measuring the price elasticity of demand.
Suitable for Nonlinear Curves
The midpoint method is useful or suitable for nonlinear curves where the traditional percentage change formula provides imprecise outcomes. The midpoint method only deals with curved demand or supply tasks functionally.
Widely Accepted
The midpoint method is widely used in education for academic research, economic analysis, or other policy-making decisions. The frequent and precise elasticity measurement makes the midpoint method a beneficial tool for understanding market dynamics.
Disadvantages of the Midpoint Method
The following are some disadvantages of the midpoint method, which are explained as follows:
Limited to Straight Lines
The midpoint method is not useful for nonlinear demand curves. This method only gives accurate measurement of PED when the points are on a straight-line demand curve.
Some Factors are Ignored
The midpoint method is used to calculate PED by using two given points. It ignores some factors such as the slope or gradient of the demand curve and the distance between the two points while calculating the price elasticity of demand.
Not Suitable More than Two Points
The midpoint method is not suitable for calculating PED if more than two given points on a demand curve are to be used.
Midpoint Formula in Geometry
In geometry, the midpoint formula is used to find the coordinates of the midpoint of two given points. Here is the midpoint formula used in geometry.
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
The midpoint method used in economics is based on the above formula used in geometry.
Conclusion
In conclusion, the midpoint method is used to calculate the price elasticity of demand or the price elasticity of supply by taking the average values of the prices and the quantities demanded. We can compute the midpoint elasticity by using the six steps explained above. The purpose of the midpoint method is to eliminate bias and make consistent comparisons, and it is a widely accepted method of calculating the price elasticity of demand. The midpoint method is limited to straight lines or to only two points of the demand curve or the supply curve.


