The Fisher Effect

The Fisher Effect illustrates the link between real interest rates, nominal interest rates and inflation.

Overview

1. Defining the Fisher Effect and the mathematical relationship it describes.
2. Practical Example (UK data).
3. Unpacking Interest Rates.
4. Limitations of the Fisher Effect.

Definition

The Fisher Effect states that real interest rates are equal to nominal interest rates, minus the expected rate of inflation. It takes its name from Irving Fisher who was the first to observe the relationship.

The Fisher Effect can be shown mathematically by the Fisher Equation:

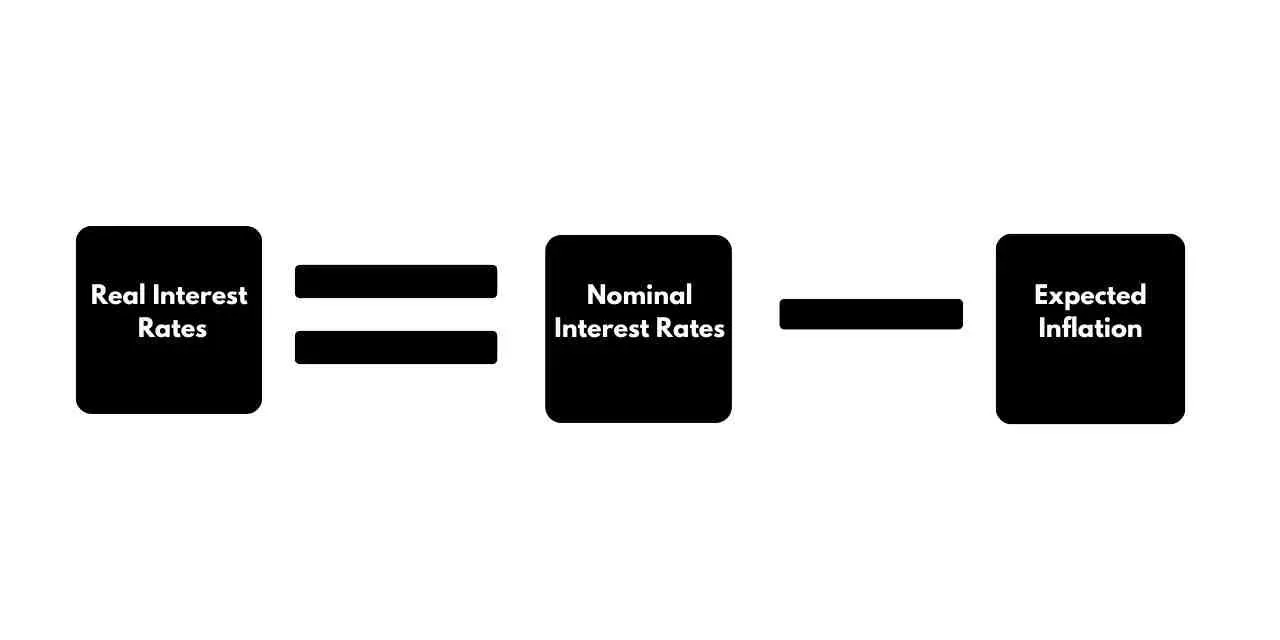
Nominal interest rates are the rates set by the central bank, as part of their Monetary Policy. Expected inflation shows how much individuals believe prices will increase in the next time period.

Example of the Fisher Effect

Below we investigate the Fisher Effect using data for the UK. As of September 2022, inflation is about 9%, meanwhile the Bank of England has just raised interest rates to 2.25%, as shown in these graphs.

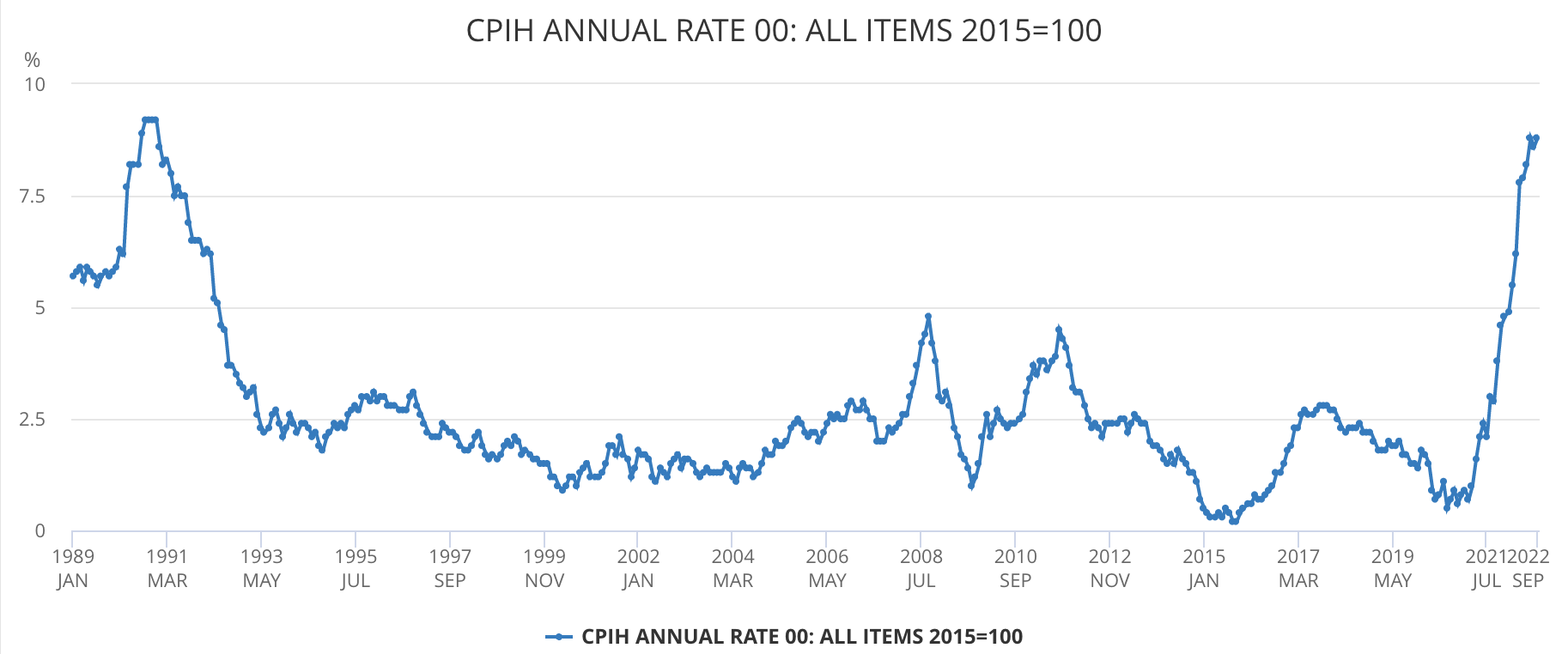
This graph from the ONS (Office of National Statistics) shows UK inflation over time with a substantial increase after February 2020 as the UK went into a cost-of-living crisis.

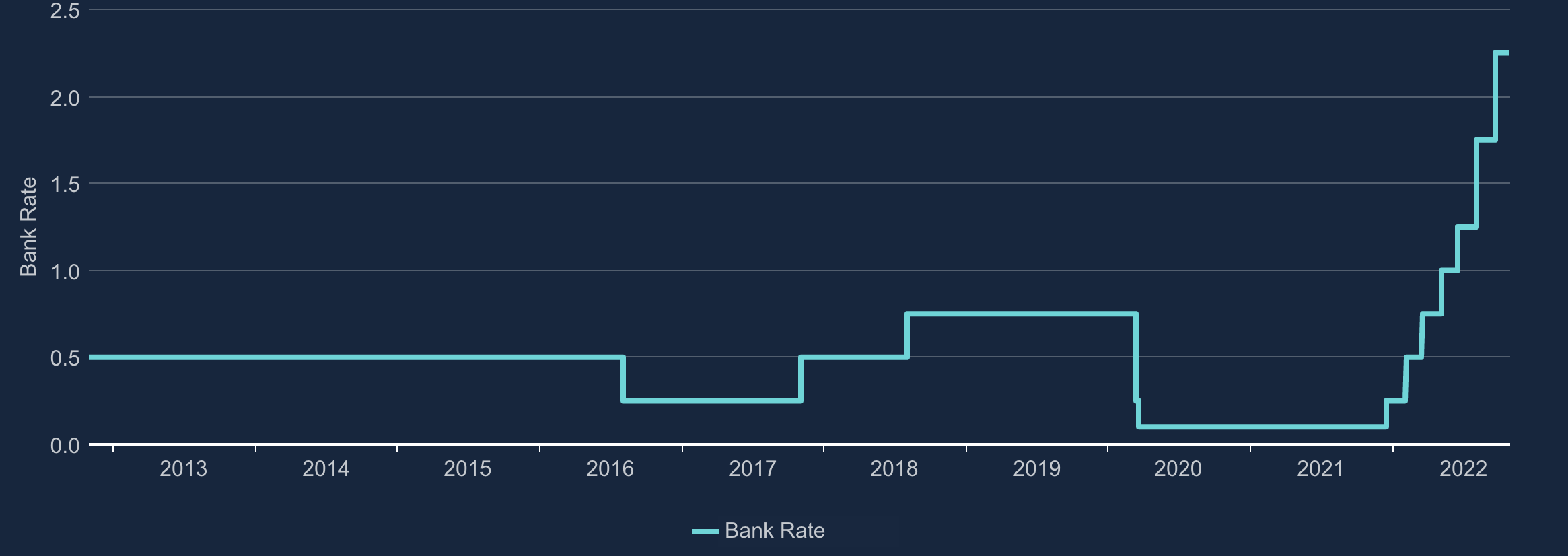
This graph shows the nominal interest rate, or base rate, set by the Bank of England. Having been almost zero since the Financial Crisis, the Bank of England has only recently started trying to limit the money supply by increasing the base rate again.

Using the Fisher Equation, what is the current level of real interest rates?

Using the data above, real interest rates = 2.25% – 9% = -6.75%

As an exercise try to work out real interest rates is 2015, and think about what they mean for the economy.

Unpacking Interest Rates

What do real interest rates mean for the Economy?

Imagine you are given £100 – what is that money worth? Today, it is worth £100 as you can buy £100-worth of things with it. Alternatively you could save it in the bank to spend in one year. If you decide to save it, you will have £102.25 next year as a result of the 2.25%  nominal interest rate. That being said, the items you could’ve bought last year have increased in value as well – because of inflation they now cost £109. Buying the items at this point would result in a 'loss' of an additional £6.75, as prices grew more in one year than your money did. As a result the 'real' interest rate, which takes inflation into account, is negative at -6.75%.

Most people would rather consume today than save their money only for it to diminish in value in real terms. Thus, consumers are encouraged to spend more (for exactly the reason shown in this scenario). If the real interest rate was positive, then by saving money individuals could increase their consumption in the future, which is an incentive for them to save. If consumption is increasing today because of negative real interest rates, what happens to aggregate demand? The increase in spending represents a positive demand shock, so demand will shift outwards, thus further increasing the price level.

Interest Rates vs Inflation

This relationship helps us understand why central banks raise nominal interest rates to combat inflation. To prevent further spending from consumers, real interest rates should be at 0%. By increasing the nominal interest rate central banks can close the gap between inflation and the base rate, calming the economy.

Using the same logic, central banks should be able to stimulate the economy by reducing the nominal interest rate. With our example, if nominal interest rates were 0%, then real interest rates would be -9% and consumers would have even more incentive to spend their money rather than saving it.

Limitations

One weakness of the use of nominal interest rates to stimulate the economy occurs when nominal interest rates are already at 0% - the Zero Lower Bound. In this setting, central banks are unable to lower rates any more – they are already at 0%, so they are forced to use alternative methods to stimulate the economy, including Quantitative Easing.

Another situation where this relationship breaks down is the Liquidity Trap. In this scenario, the conditions of the economy are so poor that consumers and businesses would rather save their money, even if they are losing some of it in real terms.